Today we are going to explain What is queue in C++? Operations of queue like enqueue and dequeue operation. Also the Limitations of Arrays and its benefits. The types of queue (priority and circular).
what is queue
A queue in C++ is a linear data structure that follows the First-In-First-Out (FIFO) principle. It means the element that enters the queue first will also leave the queue first. Just like a line in the physical world, where the person who arrives first is served first.
Real-World Examples
- Task Processing: Imagine a printer queue where documents are printed in the order they are received. The document sent first will be printed first, following the FIFO principle.
- Breadth-First Search (BFS): Queues are widely used in graph traversal algorithms like BFS. Nodes are explored in layers, with each layer representing a level of distance from the starting point.
Applications of queue in C++
- Operating Systems: Queues are used by operating systems to manage processes awaiting execution. Various scheduling algorithms like First-Come-First-Served (FCFS) and Round Robin utilize queues to determine the order of process execution.
- Networking: Routers use queues to manage incoming data packets, ensuring they are processed and forwarded in the appropriate order.
- Web Servers: Web servers often utilize queues to manage incoming HTTP requests from clients. Queues help balance the load on the server and ensure efficient request processing.
Implementation of queue
Queue in C++ can be implemented using various data structures such as arrays, linked lists, or even specialized data structures like priority queues and circular queues.
- Array-based Queue: Simple to implement but may require resizing if the array becomes full.
- Linked List Queue: Offers dynamic memory allocation and efficient enqueue and dequeue operations.
- Priority Queue: Extends the basic queue concept by assigning a priority to each element, allowing higher priority elements to be dequeued first.
- Circular Queue: In a circular queue, the last element is connected to the first element to form a circle, allowing efficient use of space and enabling cyclic behavior.
Operations of queue in C++ using Array
Enqueue Operation: The
enqueue()function Adds elements to the back of the queue, checking for overflow conditionsDequeue Operation: The
dequeue()function Removes elements from the front of the queue, ensuring the queue is not empty.Peek Operation: The
peek()function returns the element at the front of the queue without removing it.Empty Check: The
empty()function checks if the queue is empty by inspecting the front pointer.
void enqueue(int number) {
if (back == MAX_SIZE - 1) {
cout << "Queue is full" << endl;
return;
}
if (front == -1) {
// If queue is empty, set front to 0
front = 0;
}
// Increment back index and add element to the array
arr[++back] = number;
}
void dequeue() {
if (front == -1 || front > back) {
cout << "Queue is empty" << endl;
return;
}
// Increment front index to remove the element
front++;
}
Conclusion of what is queue in C++?
Queue implementation using arrays in C++ provides a simple yet powerful solution for managing sequential data processing. By understanding the underlying principles and operations of queues, programmers can design efficient algorithms and systems tailored to specific requirements.
Note
Get the Project Files from GitHub.
You can also download its Zip File by clicking on Download button.
FAQ
How is a queue in C++ different from a stack?
While both queues and stacks are linear data structures, they differ in their principle of operation. A stack follows the Last-In-First-Out (LIFO) principle, In contrast, a queue follows the FIFO principle, as described earlier.
How does a queue handle overflow and underflow conditions?
Overflow occurs when trying to add an element to a full queue, while underflow occurs when trying to remove an element from an empty queue. Queue implementations typically include checks to prevent these conditions and provide appropriate error messages or handling mechanisms.
What is the time complexity of queue operations?
The time complexity of queue operations varies depending on the implementation. In most cases, enqueue and dequeue operations have a constant time complexity of O(1), making them efficient for real-time processing. However, certain implementations, such as priority queues, may have different time complexities for specific operations.
Code of operations of Stack in C++ using Array
#include <iostream>
using namespace std;
//#define MAX_SIZE 100
const int MAX_SIZE = 100; // Maximum size of the queue array
class Queue {
int arr[MAX_SIZE]; // Array to store queue elements
int front; // Index of the front element
int back; // Index of the back element
public:
Queue() {
front = -1; // Initialize front index to -1 (empty queue)
back = -1; // Initialize back index to -1 (empty queue)
}
void enqueue(int number) {
if (back == MAX_SIZE - 1) {
cout << "Queue is full" << endl;
return;
}
if (front == -1) {
// If queue is empty, set front to 0
front = 0;
}
// Increment back index and add element to the array
arr[++back] = number;
}
void dequeue() {
if (front == -1 || front > back) {
cout << "Queue is empty" << endl;
return;
}
// Increment front index to remove the element
front++;
}
int peek() {
if (front == -1 || front > back) {
cout << "Queue is empty" << endl;
return -1;
}
// Return the front element of the queue
return arr[front];
}
bool empty() {
return (front == -1 || front > back);
}
};
int main() {
Queue q;
// Enqueue some elements
q.enqueue(1);
q.enqueue(2);
q.enqueue(3);
q.enqueue(4);
// Display the element at the front of the queue
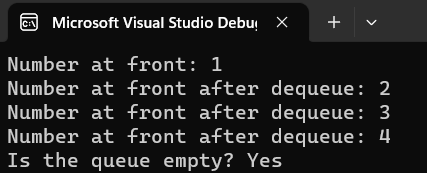
cout << "Number at front: " << q.peek() << endl;
// Dequeue elements and display the front of the queue after each dequeue operation
q.dequeue();
cout << "Number at front after dequeue: " << q.peek() << endl;
q.dequeue();
cout << "Number at front after dequeue: " << q.peek() << endl;
q.dequeue();
cout << "Number at front after dequeue: " << q.peek() << endl;
q.dequeue();
// Check if the queue is empty
cout << "Is the queue empty? " << (q.empty() ? "Yes" : "No") << endl;
return 0;
}
