What are the prefix and postfix expressions?

Prefix to postfix are notations used to represent the expressions. These notations determine the placement of operators and operands in an expression.

Prefix Expression: In prefix notation, also known as Polish notation, the operator precedes its operands. This notation eliminates the need for parentheses to indicate the order of operations.

Postfix Expression: In postfix notation, also known as Reverse Polish notation (RPN), the operator follows its operands. Like prefix notation, postfix notation eliminates the need for parentheses to indicate the order of operations.

Comparison:

• Prefix Notation: Operators come before their operands.
• Postfix Notation: Operators come after their operands.

conversion of prefix to postfix in C++ using stack

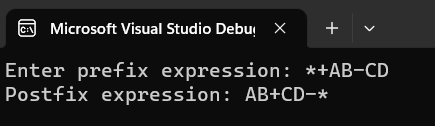
conversion of prefix to postfix in C++ using stack of this given *+AB-CD can be written as:

Explanation:

1. Expression: *+AB-CD
2. Traverse the Prefix Expression from Right to Left:
   • Start from the rightmost character of the prefix expression.
3. Read Characters:
   • Read D. As D is an operand, push it onto the stack.
     • Stack: D
   • Read C. As C is an operand, push it onto the stack.
     • Stack: D C
   • Read -. As - is an operator, pop two operands from the stack (D and C). Concatenate them with the operator - and push the result ((D-C)) back onto the stack.
     • Stack: (D-C)
   • Read B. As B is an operand, push it onto the stack.
     • Stack: (D-C) B
   • Read A. As A is an operand, push it onto the stack.
     • Stack: (D-C) B A
   • Read +. As + is an operator, pop two operands from the stack (B and A). Concatenate them with the operator + and push the result ((B+A)) back onto the stack.
     • Stack: (D-C) (B+A)
   • Read *. As * is an operator, pop two operands from the stack ((B+A) and (D-C)). Concatenate them with the operator * and push the result (((B+A)*(D-C))) back onto the stack.
     • Stack: ((B+A)*(D-C))
4. Final Result:
   • The infix expression obtained from the prefix expression *+AB-CD is ((B+A)*(D-C)).

Source code of conversion Prefix to postfix C++ using stack

#include <iostream>
#include <stack>
#include <string>

using namespace std;

// Function to check if the given character is an operand
bool isOperand(char c) {
    return (c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z') || (c >= '0' && c <= '9');
}

// Function to convert prefix expression to postfix expression
string prefixToPostfix(string prefix) {
    stack<string> s;

    // Traverse the prefix expression from right to left
    for (int i = prefix.length() - 1; i >= 0; i--) {
        if (isOperand(prefix[i])) {
            // Push operands to the stack
            s.push(string(1, prefix[i]));
        }
        else {
            // Pop two operands from the stack
            string op1 = s.top(); s.pop();
            string op2 = s.top(); s.pop();

            // Concatenate operands and the operator
            string temp = op1 + op2 + prefix[i];

            // Push the result back to the stack
            s.push(temp);
        }
    }

    return s.top();
}

int main() {
    string prefix;

    cout << "Enter prefix expression: ";
    getline(cin, prefix);

    string postfix = prefixToPostfix(prefix);

    cout << "Postfix expression: " << postfix << endl;

    return 0;
}

Conclusion

Prefix to postfix conversion is a fundamental concept in computer science and mathematics that involves transforming expressions from prefix notation (Polish notation) to postfix notation (Reverse Polish notation). This conversion simplifies the evaluation and parsing of arithmetic expressions by rearranging the placement of operators and operands.

FAQ