Understanding the Basics

Before diving into the intricacies of infix to postfix conversion, let’s clarify the fundamental concepts involved.

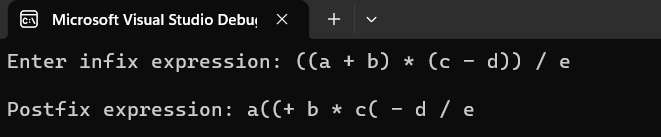
• Infix Notation: Infix notation is the standard arithmetic notation that we’re all familiar with. In this notation, operators are placed between operands, such as ((a + b) * (c - d)) / e.
• Postfix Notation: Postfix notation, also known as Reverse Polish Notation (RPN), positions operators after their operands, like a b + c d - * e /.

Conversion of infix to postfix in C++ using stack

Here is the key reasons of why conversion of infix to postfix in C++ using stack is needed :

Initialize an Empty Stack

We’ll use a stack to temporarily store operators and parentheses during the conversion process.

Traverse the Infix Expression

Start scanning the infix expression from left to right. At each step, perform the following actions:

• If the current character is an operand (variable), push it to the output string.
• If the current character is a left parenthesis (, push it onto the stack.
• If the current character is a right parenthesis ), pop operators from the stack and append them to the output string until a matching left parenthesis is encountered. Discard the left parenthesis.
• If the current character is an operator (+, -, *, /), compare its precedence with the operator at the top of the stack. If the current operator has higher precedence or the stack is empty, push the current operator onto the stack. Otherwise, pop operators from the stack.

Repeat this process until all characters in the infix expression have been processed. After processing all characters, pop any remaining operators from the stack and append them to the output string.

Principles of Conversion infix to postfix

The process of converting an infix to postfix notation involves rearranging the operators and operands while preserving the expression’s original meaning. Here are the key principles involved:

Operator Precedence

Operators have different precedence levels, with some taking precedence over others. For example, multiplication and division typically have higher precedence than addition and subtraction.

Parentheses Handling

Parentheses affect the order of evaluation in infix expressions. When converting to postfix notation, we need to handle parentheses to ensure the correct order of operations.

Application of this conversion

• Expression Evaluation: Postfix notation simplifies the process of evaluating mathematical expressions. By converting infix expressions to postfix, we eliminate the need for parentheses and precedence rules, making the evaluation algorithm simpler and more efficient.
• Compiler Design: In compilers and programming language interpreters, infix to postfix conversion is a crucial step in the lexical analysis phase. It helps in transforming human-readable expressions into a format that is easier for machines to process and execute.
• Digital Circuit Design: In digital circuit design and logic synthesis, postfix notation is used to represent Boolean expressions and logic equations. Converting infix expressions to postfix helps in simplifying and optimizing the design of digital circuits.

Conclusion of infix to postfix C++ using stack

Mastering infix to postfix conversion is a valuable skill for any programmer. By exploring the principles, techniques, and practical considerations outlined in this guide, you’ll be well-equipped to tackle infix to postfix conversion challenges with confidence. Whether you’re building a calculator application, designing a compiler, or exploring the depths of algorithmic problem-solving, infix to postfix conversion is sure to be a valuable addition to your toolkit.

Source Code

Let’s break down the provided C++ code snippet that handles the infix to postfix conversion:

#include <iostream>
#include <stack>
#include <string>

using namespace std;

int precedence(char c) {
    if (c == '^') {
        return 3;
    }
    else if (c == '*' || c == '/') {
        return 2;
    }
    else if (c == '+' || c == '-') {
        return 1;
    }
    else {
        return -1;
    }
}

string infixToPostfix(string s) {
    stack<char> st;
    string res;

    for (int i = 0; i < s.length(); i++) {
        if ((s[i] >= 'a' && s[i] <= 'z') || (s[i] >= 'A' && s[i] <= 'Z')) {
            res += s[i];
        }
        else if (s[i] == '(') {
            st.push(s[i]);
        }
        else if (s[i] == ')') {
            while (!st.empty() && st.top() != '(') {
                res += st.top();
                st.pop();
            }
            if (!st.empty()) {
                st.pop();
            }
        }
        else {
            while (!st.empty() && precedence(st.top()) >= precedence(s[i])) {
                res += st.top();
                st.pop();
            }
            st.push(s[i]);
        }
    }

    while (!st.empty()) {
        res += st.top();
        st.pop();
    }

    return res;
}

int main() {
    string s;
    cout << "Enter infix expression: ";
    getline(cin, s);

    string postfix = infixToPostfix(s);
    cout << endl;
    cout << "Postfix expression: " << postfix << endl;

    return 0;
}