The C++ Time Complexity Analyzer makes this process simpler by analyzing your code and determining its time complexity step by step. Whether you’re a beginner or an experienced developer, this tool offers clarity on how your code performs.
What Does the Analyzer Do?
This program reads your C++ code line by line, identifies patterns like loops, recursion, and function calls, and categorizes each line into one of the standard time complexities:
- O(1): Constant time, e.g., a single arithmetic operation.
- O(n): Linear time, e.g., a loop iterating over n elements.
- O(n²): Quadratic time, e.g., nested loops.
- O(n³): Cubic time, e.g., triple-nested loops.
- O(n \log n): Divide-and-conquer patterns, e.g., merge sort.
The program also provides a reason for each categorization, which helps you understand why a line is categorized as such.
NOTE
You can get the code of C++ time complexity analyzer from my GitHub repository
How Does It Work?
Step 1: Accepting User Input
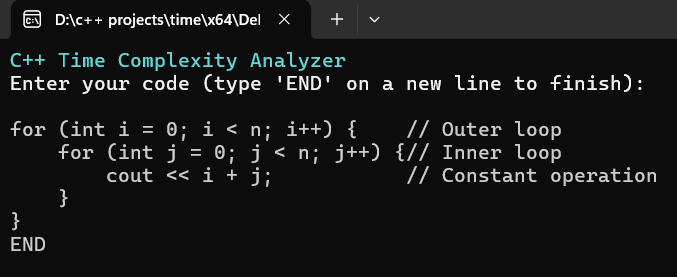
The program starts by asking the user to input their code. You can type or paste multiple lines, and when you’re done, type END to signal the end of your input. For example:
C++ Time Complexity Analyzer
Enter your code (type 'END' on a new line to finish):
for (int i = 0; i < n; i++) { // Outer loop
for (int j = 0; j < n; j++) {// Inner loop
cout << i + j; // Constant operation
}
}
END
Step 2: Parsing the Code
The program processes each line:
- Whitespace Removal: Trims unnecessary spaces for easier analysis.
- Comment Filtering: Skips lines that are comments (starting with
//) or empty lines.
Step 3: Analyzing Each Line
Each line is analyzed to determine its time complexity. Here’s how the tool approaches it:
a. Identifying Loops
Loops are detected using patterns like for or while. The tool checks how deeply loops are nested:
- Single loop: O(n)
- Two nested loops: O(n²)
- Three nested loops: O(n³)
Example:
for (int i = 0; i < n; i++) { // Outer loop: O(n)
for (int j = 0; j < n; j++) { // Inner loop: O(n²)
// Work here
}
}
b. Recognizing Recursive Functions
Recursion is identified by detecting function calls to the same function within its body. Recursive functions often exhibit logarithmic or linearithmic complexity depending on their implementation.
Example:
int factorial(int n) {
if (n == 0) return 1;
return n * factorial(n - 1); // Recursive call: O(n)
}
c. Handling Function Calls
Function calls are identified but their complexity is marked as UNKNOWN unless their implementation is provided.
Example:
void process() {
doWork(); // Function call: UNKNOWN
}
d. Simplifying Simple Operations
Lines without loops, recursion, or function calls are categorized as O(1) because their execution time is constant.
Example:
int x = 5 + 3; // O(1): Arithmetic operation
Step 4: Tracking Nesting Levels
The program uses a stack to track the depth of code blocks ({}) and loops. This is important because the maximum nesting level determines the overall time complexity of the code.
For example:
for (int i = 0; i < n; i++) { // Level 1: O(n)
for (int j = 0; j < n; j++) { // Level 2: O(n²)
for (int k = 0; k < n; k++) { // Level 3: O(n³)
// Work
}
}
}
Here, the maximum nesting level is 3, so the overall complexity is O(n3)O(n³).
Step 5: Generating Output
For every line of code, the program outputs:
- Line Number: Helps you locate the analyzed line.
- Original Code: The exact code on that line.
- Complexity: The estimated time complexity, displayed in colored text for easy interpretation.
- Reason: A detailed explanation of the complexity.
Example Output:
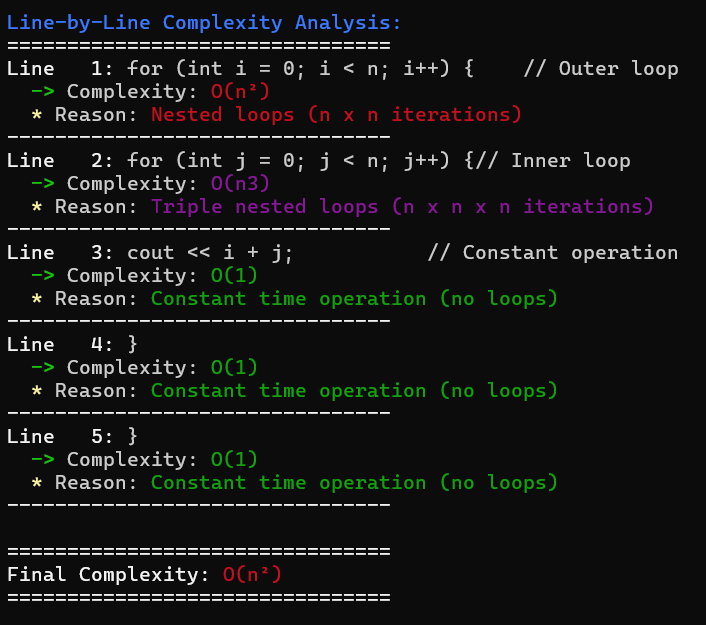
Estimating Overall Complexity
Once all lines are analyzed, the program determines the overall complexity by evaluating the deepest nesting level in the code. It uses the following rules:
- 0 nesting levels → O(1)
- 1 nesting level → O(n)
- 2 nesting levels → O(n²)
- 3 nesting levels → O(n³)
If recursion is detected, the overall complexity may also be O(nlogn)O(n \log n) or similar.
Why Use This Analyzer?
- Improve Code Efficiency: Spot inefficiencies in your loops and recursion easily.
- Learn Algorithm Design: Understand how your coding patterns affect performance.
- Educational Tool: Perfect for beginners learning about time complexity.
- Debugging Aid: Identify bottlenecks in competitive programming or software projects.
Technical Highlights
Key Functions
analyze_line- Determines the complexity of a single line.
- Detects loops, recursion, and function calls.
track_function_definitions- Maps function definitions to enable recursive call detection.
get_complexity_reason- Provides detailed reasoning for the complexity of a line, making it easier to understand inefficiencies.
Output
The tool uses ANSI color codes for a visually appealing terminal output:
- Green for constant time (
O(1)). - Yellow for linear time (
O(n)). - Red for quadratic time (
O(n²)), and so on.
Nesting Level
The nesting level is tracked using a stack. Each block (e.g., { or for) increases the level, and closing blocks (}) reduce it. This ensures accurate estimation of deeply nested constructs.
Limitations
While the analyzer is powerful, it has a few limitations:
- Function Calls: It cannot determine the complexity of function calls without their implementation.
- Assumptions: It assumes all loops iterate n times, which may not always be true.
- Context Ignorance: It doesn’t account for conditional logic or input constraints.
Conclusion
The C++ Time Complexity Analyzer is a smart and intuitive tool to help developers write better code. By breaking down time complexity line by line, it provides insights into how algorithms scale, making it an invaluable resource for students, developers, and competitive programmers alike.
Source code of Time complexity analysis tool
#include <iostream>
#include <string>
#include <vector>
#include <regex>
#include <stack>
#include <unordered_map>
#include <iomanip>
#include <locale>
using namespace std;
// ANSI color codes
#define RESET "\033[0m"
#define RED "\033[31m"
#define GREEN "\033[32m"
#define YELLOW "\033[33m"
#define BLUE "\033[34m"
#define MAGENTA "\033[35m"
#define CYAN "\033[36m"
#define WHITE "\033[37m"
#define BOLD "\033[1m"
#define UNDERLINE "\033[4m"
// Time complexity enumeration
enum class Complexity {
CONSTANT, // O(1)
LINEAR, // O(n)
QUADRATIC, // O(n²)
CUBIC, // O(n³)
LINEARITHMIC, // O(n log n)
UNKNOWN
};
// Structure to hold analysis results
struct CodeAnalysis {
int line_number;
string code;
Complexity complexity;
string reason;
};
class ComplexityAnalyzer {
private:
vector<string> code_lines;
unordered_map<string, int> function_calls;
stack<string> block_stack;
string current_function;
int nesting_level = 0;
int max_nesting = 0;
// Helper function to trim whitespace
static string trim(const string& str) {
const regex pattern("^\\s+|\\s+$");
return regex_replace(str, pattern, "");
}
// Check if line is a comment
static bool is_comment(const string& line) {
return line.empty() || line.substr(0, 2) == "//";
}
// Detect recursive function calls
bool is_recursive(const string& line, const string& func_name) const {
if (func_name.empty()) return false;
return regex_search(line, regex("\\b" + func_name + "\\s*\\("));
}
// Track function definitions in the code
void track_function_definitions() {
for (const auto& line : code_lines) {
smatch match;
if (regex_search(line, match, regex(R"(\b([a-zA-Z_][a-zA-Z0-9_]*)\s*\([^)]*\)\s*(?:const)?\s*[{;])"))) {
function_calls[match[1].str()]++;
}
}
}
public:
explicit ComplexityAnalyzer(const vector<string>& code) : code_lines(code) {}
// Convert complexity enum to string with color
static string complexity_to_string(Complexity c) {
switch (c) {
case Complexity::CONSTANT: return GREEN + string("O(1)") + RESET;
case Complexity::LINEAR: return YELLOW + string("O(n)") + RESET;
case Complexity::QUADRATIC: return RED + string("O(n²)") + RESET;
case Complexity::CUBIC: return MAGENTA + string("O(n³)") + RESET;
case Complexity::LINEARITHMIC: return CYAN + string("O(n log n)") + RESET;
default: return WHITE + string("Unknown") + RESET;
}
}
// Get explanation for the complexity with color
string get_complexity_reason(const string& line, Complexity complexity) const {
switch (complexity) {
case Complexity::CONSTANT:
return GREEN + string("Constant time operation (no loops)") + RESET;
case Complexity::LINEAR:
if (regex_search(line, regex(R"(\b(for|while)\s*\()"))) {
return YELLOW + string("Single loop running n times") + RESET;
}
return YELLOW + string("Linear time operation") + RESET;
case Complexity::QUADRATIC:
return RED + string("Nested loops (n × n iterations)") + RESET;
case Complexity::CUBIC:
return MAGENTA + string("Triple nested loops (n × n × n iterations)") + RESET;
case Complexity::LINEARITHMIC:
return CYAN + string("Divide-and-conquer or recursive algorithm") + RESET;
default:
return WHITE + string("Unable to determine complexity") + RESET;
}
}
// Analyze a single line of code
Complexity analyze_line(const string& line) {
if (is_comment(line)) return Complexity::CONSTANT;
// Check for loops
if (regex_search(line, regex(R"(\b(for|while)\s*\()"))) {
if (nesting_level == 0) return Complexity::LINEAR;
if (nesting_level == 1) return Complexity::QUADRATIC;
return Complexity::CUBIC;
}
// Check for recursion
if (!current_function.empty() && is_recursive(line, current_function)) {
return Complexity::LINEARITHMIC;
}
// Check for function calls
if (regex_search(line, regex(R"(\b[a-zA-Z_][a-zA-Z0-9_]*\s*\([^)]*\)\s*;)"))) {
return Complexity::UNKNOWN;
}
return Complexity::CONSTANT;
}
// Analyze the entire code
vector<CodeAnalysis> analyze() {
vector<CodeAnalysis> results;
track_function_definitions();
for (size_t i = 0; i < code_lines.size(); ++i) {
string line = trim(code_lines[i]);
// Track function declarations
smatch match;
if (regex_search(line, match, regex(R"(\b([a-zA-Z_][a-zA-Z0-9_]*)\s*\([^)]*\)\s*(?:const)?\s*[{])"))) {
current_function = match[1].str();
}
// Track block openings
if (regex_search(line, regex(R"(\b(for|while)\s*\()"))) {
block_stack.push("loop");
nesting_level++;
max_nesting = max(max_nesting, nesting_level);
}
else if (line.find('{') != string::npos) {
block_stack.push("block");
}
// Analyze the line
Complexity comp = analyze_line(line);
results.push_back({
static_cast<int>(i + 1),
line,
comp,
get_complexity_reason(line, comp)
});
// Track block closings
if (line.find('}') != string::npos && !block_stack.empty()) {
if (block_stack.top() == "loop") nesting_level--;
block_stack.pop();
}
}
return results;
}
// Estimate overall complexity based on max nesting
Complexity estimate_overall_complexity() const {
switch (max_nesting) {
case 0: return Complexity::CONSTANT;
case 1: return Complexity::LINEAR;
case 2: return Complexity::QUADRATIC;
case 3: return Complexity::CUBIC;
default: return Complexity::LINEARITHMIC;
}
}
};
// Print analysis results with colored ASCII formatting
void print_results(const vector<CodeAnalysis>& results) {
cout << "\n" << BOLD << BLUE << "Line-by-Line Complexity Analysis:" << RESET << "\n";
cout << BOLD << "================================" << RESET << "\n";
for (const auto& result : results) {
cout << BOLD << "Line " << setw(3) << result.line_number << ": " << RESET
<< WHITE << result.code << RESET << "\n";
cout << " " << BOLD << GREEN << "->" << RESET << " Complexity: "
<< ComplexityAnalyzer::complexity_to_string(result.complexity) << "\n";
cout << " " << BOLD << YELLOW << "* " << RESET << "Reason: " << result.reason << "\n";
cout << BOLD << "--------------------------------" << RESET << "\n";
}
}
// Print final complexity with colored ASCII formatting
void print_final_complexity(Complexity complexity) {
cout << "\n" << BOLD << "================================" << RESET << "\n";
cout << BOLD << "Final Complexity: " << RESET
<< ComplexityAnalyzer::complexity_to_string(complexity) << "\n";
cout << BOLD << "================================" << RESET << "\n";
}
int main() {
// Set locale for consistent output
ios_base::sync_with_stdio(false);
locale::global(locale(""));
cout.imbue(locale());
cout << BOLD << CYAN << "C++ Time Complexity Analyzer" << RESET << "\n";
cout << BOLD << "Enter your code (type 'END' on a new line to finish):" << RESET << "\n\n";
// Read input code
vector<string> code;
string line;
while (getline(cin, line) && line != "END") {
code.push_back(line);
}
// Analyze and display results
ComplexityAnalyzer analyzer(code);
auto results = analyzer.analyze();
print_results(results);
print_final_complexity(analyzer.estimate_overall_complexity());
return 0;
}


This will be very helpful for DAA, thank you!