Explore a C++ project of maze solver using algorithms like Depth-First Search (DFS) or Breadth-First Search (BFS). Discover how to navigate mazes, mark paths, and find solutions programmatically in this detailed example.
Introduction
Navigating through a maze is a classic problem that has fascinated humans for centuries, whether it’s a hedge maze in a garden or a logical puzzle on paper. With the advent of computers, we can leverage algorithms to solve these problems more efficiently and reliably. This blog post will guide you through a simple C++ implementation of a maze solver using Depth-First Search (DFS). We’ll also discuss how this algorithm works and demonstrate its application with an example.
Solving Mazes with Depth-First Search in C++
Depth-First Search is a fundamental algorithm in computer science used for traversing or searching tree or graph data structures. It explores as far as possible along each branch before backtracking, which makes it ideal for maze-solving problems. The core idea is to start at the root (or any arbitrary node), explore each branch to its deepest point, and then backtrack to explore the next branch.
Steps to Solve the Maze Solver in C++
- Maze Representation:
- The maze is represented as a 2D array (vector of vectors in C++).
- Each cell in the array can be a path (
0), a wall (1), or the goal (2).
- Input and Output:
- The user inputs the maze dimensions, the maze structure, and the starting position.
- The program outputs the maze with the path from the start to the goal, if one exists.
- Algorithm Details:
- The DFS algorithm starts at the specified starting position and recursively explores each possible direction (right, down, left, up).
- It marks the current cell as part of the path and checks if it has reached the goal.
- If a dead-end is encountered, it backtracks to explore other possible paths.
Note
get the Source code of maze solver project from GitHub
Implementation Breakdown
1. Defining Directions for Movement
To navigate through the maze, we define possible movements in four directions: right, down, left, and up. This is accomplished using a vector of pairs, where each pair represents a movement in the x and y directions.
const std::vector<std::pair<int, int>> directions = {
{0, 1}, // Right
{1, 0}, // Down
{0, -1}, // Left
{-1, 0} // Up
};
2. Printing the Maze
A function is provided to print the maze in a readable format. Paths are marked with *, making it easy to visualize the solution.
void printMaze(const std::vector<std::vector<int>>& maze) {
for (const auto& row : maze) {
for (int cell : row) {
if (cell == -1) {
std::cout << "* "; // Path
} else {
std::cout << cell << " ";
}
}
std::cout << std::endl;
}
}
3. Validating Moves
To ensure that we don’t move into walls or out of the maze boundaries, a validation function checks if a position is valid for movement.
bool isValid(const std::vector<std::vector<int>>& maze, int x, int y) {
return x >= 0 && x < maze.size() && y >= 0 && y < maze[0].size() && maze[x][y] == 0;
}
4. Solving the Maze with DFS
The solveMaze function implements the DFS algorithm. It recursively explores each direction from the current cell and backtracks if it encounters a dead end.
bool solveMaze(std::vector<std::vector<int>>& maze, int x, int y) {
if (maze[x][y] == 2) {
return true; // Reached the goal
}
maze[x][y] = -1; // Mark the current cell as part of the path
for (const auto& dir : directions) {
int newX = x + dir.first;
int newY = y + dir.second;
if (isValid(maze, newX, newY) && solveMaze(maze, newX, newY)) {
return true;
}
}
maze[x][y] = 0; // Backtrack: unmark the cell
return false;
}
5. Main Function for User Interaction
The main function handles user input and initiates the maze-solving process. It takes the maze dimensions, the maze itself, and the starting position as input from the user.
int main() {
int rows, cols;
std::cout << "Enter the number of rows and columns in the maze: ";
std::cin >> rows >> cols;
std::vector<std::vector<int>> maze(rows, std::vector<int>(cols));
std::cout << "Enter the maze (0 for path, 1 for wall, 2 for goal):" << std::endl;
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
std::cin >> maze[i][j];
}
}
int startX, startY;
std::cout << "Enter the starting position (row and column): ";
std::cin >> startX >> startY;
std::cout << "Maze before solving:\n";
printMaze(maze);
if (solveMaze(maze, startX, startY)) {
std::cout << "Path to the goal found:\n";
} else {
std::cout << "No path to the goal exists.\n";
}
printMaze(maze);
return 0;
}
Example of maze solver project
Here is an example run of the program, which demonstrates how the maze solver works:
0represents an open path.1represents a wall.2represents the goal.
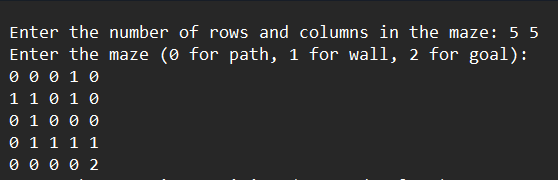
Input:
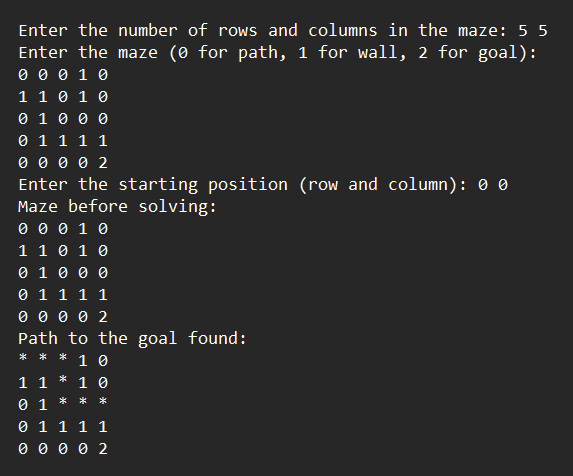
Output:
Explanation:
- Initial Maze State:
- The maze is printed before solving, showing the initial state.
- The starting position
(0, 0)is an open path (0).
- Path Finding:
- The algorithm starts at
(0, 0)and recursively explores possible paths using Depth-First Search (DFS). - It marks the cells visited along the path with
*.
- The algorithm starts at
- Solved Maze State:
- After finding the path to the goal
(4, 4), the maze is printed again, showing the path marked with*. - The output confirms that a path from
(0, 0)to(4, 4)exists.
- After finding the path to the goal
Conclusion
This C++ maze solver using DFS is a great example of how simple algorithms can be used to tackle seemingly complex problems. The flexibility of the code allows it to be easily adapted for different maze sizes and structures. By understanding the principles of DFS and backtracking, you can apply these techniques to a wide variety of other problems in computer science and beyond.
Source code of C++ project of maze solver
#include <iostream>
#include <vector>
// Define the directions for moving in the maze (right, down, left, up)
const std::vector<std::pair<int, int>> directions = {
{0, 1}, // Right
{1, 0}, // Down
{0, -1}, // Left
{-1, 0} // Up
};
// Function to print the maze
void printMaze(const std::vector<std::vector<int>>& maze) {
for (const auto& row : maze) {
for (int cell : row) {
if (cell == -1) {
std::cout << "* "; // Path
}
else {
std::cout << cell << " ";
}
}
std::cout << std::endl;
}
}
// Function to check if a position is within the maze and not a wall
bool isValid(const std::vector<std::vector<int>>& maze, int x, int y) {
return x >= 0 && x < maze.size() && y >= 0 && y < maze[0].size() && maze[x][y] == 0;
}
// Depth-First Search to solve the maze
bool solveMaze(std::vector<std::vector<int>>& maze, int x, int y) {
if (maze[x][y] == 2) {
return true; // Reached the goal
}
// Mark the current cell as part of the path
maze[x][y] = -1;
for (const auto& dir : directions) {
int newX = x + dir.first;
int newY = y + dir.second;
if (isValid(maze, newX, newY) && solveMaze(maze, newX, newY)) {
return true;
}
}
// Backtrack: unmark the cell
maze[x][y] = 0;
return false;
}
int main() {
int rows, cols;
std::cout << "Enter the number of rows and columns in the maze: ";
std::cin >> rows >> cols;
std::vector<std::vector<int>> maze(rows, std::vector<int>(cols));
std::cout << "Enter the maze (0 for path, 1 for wall, 2 for goal):" << std::endl;
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
std::cin >> maze[i][j];
}
}
int startX, startY;
std::cout << "Enter the starting position (row and column): ";
std::cin >> startX >> startY;
std::cout << "Maze before solving:\n";
printMaze(maze);
if (solveMaze(maze, startX, startY)) {
std::cout << "Path to the goal found:\n";
}
else {
std::cout << "No path to the goal exists.\n";
}
printMaze(maze);
return 0;
}

