Welcome to our step-by-step guide on binary search tree in C++ using linked lists. They offer efficient search, insertion, traversal, and deletion operations. A binary search tree in C++ is a popular computer science and programming data structure. However, managing binary search trees can sometimes be challenging, especially when dealing with complex operations.
In this guide, we will explore how to simplify the implementation of a binary search tree by using linked lists including Insertion, Deletion, and Traversal Operations. Linked lists provide a flexible and reliable way to represent binary search trees. By understanding the underlying principles and steps involved, you can optimize code and achieve better performance.
Let us walk through the process of creating and managing binary search trees. From understanding the basic concepts to implementing key operations, such as insertion and deletion, we’ll cover everything you need to know. So, whether you’re a beginner looking to enhance your coding skills or an experienced programmer seeking optimization techniques, this guide is perfect.
Understanding the basics of binary search trees
Before Discussing the implementation using linked lists, it’s important to have a solid understanding of the basics of binary search trees. A binary search tree is a hierarchical data structure that is composed of nodes. A value and references to its left and right children are contained in every node. There is a value in the left child node that is less than the parent node and a value in the right child node that is greater than the parent node.
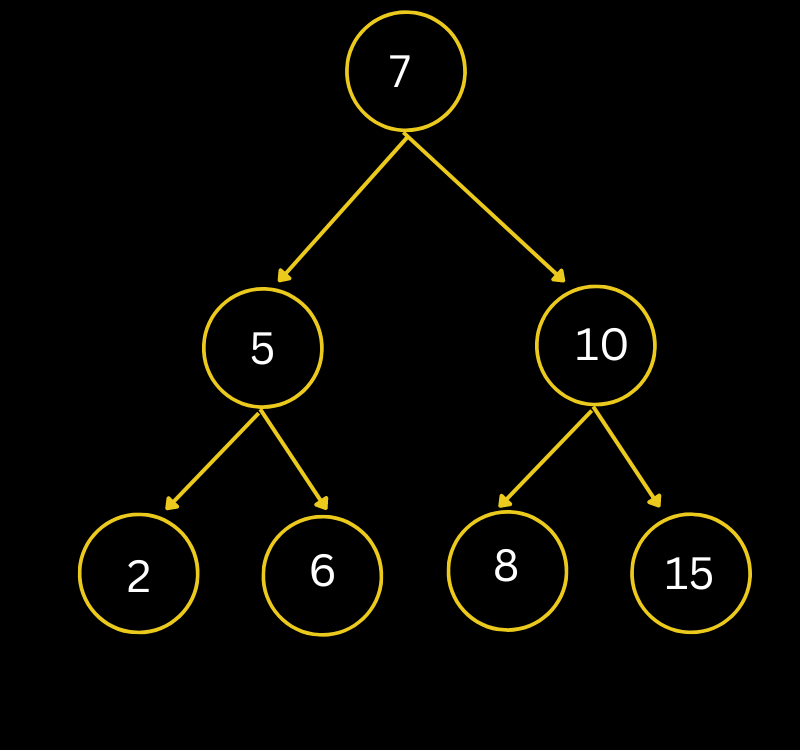
Binary search trees are ordered, which means the values are arranged in a specific order. This ordering property allows for efficient searching and other operations. In a binary search tree, the left subtree of a node contains values that are smaller than the node’s value, while the right subtree contains larger values.
Implementing a binary search tree in C++ using linked lists
Now let’s move on to implementing them using linked lists in C++. Linked lists provide a flexible and intuitive way to represent binary search trees. Instead of using pointers to the left and right children, we can use pointers to the next node in the linked list.
We first need to create a structure for the nodes to implement a binary search tree using linked lists. The node structure should contain a value and a pointer to the next node. We also need to keep track of the root node, which is the starting point of the binary search tree.
struct Node {
int value;
Node next;
};
Node root = nullptr;
Insertion operation in a binary search tree
The insertion operation is one of the most important operations in a binary search tree. The ordering property must be used to determine the proper location when adding a new value to the tree. Beginning at the root node, the insertion operation moves down the tree until it comes across a space that is free to receive the new value.
The first step in using linked lists to insert a value into the binary search tree is to create a new node with the specified value. Next, we compare the value with each node as we move through the tree. We proceed to the left child node if the value is less than the value of the current node. We proceed to the appropriate child node if the value is higher. We carry on with this procedure.
void insert(int value) {
Node newNode = new Node;
newNode->value = value;
newNode->next = nullptr;
if (root == nullptr) {
root = newNode;
return;
}
Node current = root;
while (true) {
if (value current->value) {
if (current->left == nullptr) {
current->left = newNode;
return;
}
current = current->left;
}
else {
if (current->right == nullptr) {
current->right = newNode;
return;
}
current = current->right;
}
}
}
Deletion operation in a binary search tree
Another important operation in a binary search tree is the deletion operation. When deleting a node from the tree, we need to maintain the ordering property. The deletion operation can be divided into three cases: deleting a node with no children, deleting a node with one child, and deleting a node with two children.
To delete a node from the binary search tree using linked lists, we first need to find the node we want to delete. Once we find the node, we need to handle the three cases mentioned earlier.
void remove(int value) {
if (root == nullptr)
return;
Node current = root;
Node parent = nullptr;
while (current != nullptr && current->value != value) {
parent = current;
if (value current->value)
current = current->left;
else
current = current->right;
}
if (current == nullptr)
return;
if (current->left == nullptr && current->right == nullptr) {
if (current == root)
root = nullptr;
else if (current == parent->left)
parent->left = nullptr;
else
parent->right = nullptr;
delete current;
}
else if (current->left == nullptr) {
if (current == root)
root = current->right;
else if (current == parent->left)
parent->left = current->right;
else
parent->right = current->right;
delete current;
}
else if (current->right == nullptr) {
if (current == root)
root = current->left;
else if (current == parent->left)
parent->left = current->left;
else
parent->right = current->left;
delete current;
}
else {
Node* successor = findMin(current->right);
current->value = successor->value;
remove(successor->value);
}
Traversal techniques for binary search trees
Traversal is another important aspect of working with binary search trees. There are three common traversal techniques: in-order, pre-order, and post-order. In-order traversal visits the nodes in ascending order, pre-order traversal visits the parent node before its children, and post-order traversal visits the children nodes before the parent node.
To perform in-order traversal of a binary search tree using linked lists, we can use a recursive approach. We visit the current node, traverse the left subtree first, and then traverse the right subtree.
void inorder(Node* node) {
if (node == nullptr)
return;
inorder(node->left);
// Process current node
cout node->value " ";
inorder(node->right);
Balancing binary search trees for optimal performance
Binary search trees can become unbalanced, leading to decreased performance for certain operations. Balancing a binary search tree ensures that the tree is evenly distributed, improving search, insertion, and deletion operations.
There are various balancing techniques available, such as the AVL tree and the Red-Black tree. These techniques involve performing rotations and adjustments to maintain the balance of the tree.
Advantages and disadvantages of using linked lists for binary search tree
Using linked lists to implement binary search trees has its advantages and disadvantages. One of the main advantages is the flexibility and ease of implementation. Linked lists allow for dynamic memory allocation, which can be beneficial when dealing with changing data. Additionally, linked lists can handle large amounts of data efficiently.
However, linked lists also have some disadvantages. They require more memory compared to arrays because each node needs to store a pointer to the next node. Linked lists can also have slower access times compared to arrays, especially when searching for a specific element.
Conclusion and additional resources for further learning
In conclusion, linked lists provide a simplified way to implement binary search trees in C++. By understanding the basic concepts and following the step-by-step guide, you can optimize your code and achieve better performance. We covered the basics of binary search trees, the implementation using linked lists, key operations such as insertion and deletion, searching for a value, traversal techniques, balancing, and the advantages and disadvantages of using linked lists.
If you want to implement that in your final year project then see that post also.
We hope this guide has provided you with valuable insights and practical knowledge on simplifying binary search trees using linked lists in C++. If you have any queries related to that topic, contact us below with your queries.
FAQ
1. What is a Binary Search Tree (BST)?
A Binary Search Tree is a hierarchical data structure composed of nodes. Each node contains a value and references to its left and right children. The ordering property of a BST ensures that the values in the left subtree are smaller than the parent node, while values in the right subtree are larger.
2. Why use linked lists to implement Binary Search Trees?
Linked lists offer a flexible and intuitive way to represent Binary Search Trees. Instead of using traditional pointers to the left and right children, linked lists use pointers to the next node in the list, simplifying the implementation.
3. What are the key operations in a Binary Search Tree?
The primary operations include insertion, deletion, and traversal. Insertion involves finding the correct position for a new value. Deletion maintains the ordering property and handles cases with zero, one, or two children. Traversal methods include in-order, pre-order, and post-order.
4. How is the insertion operation implemented in a BST using linked lists?
The insertion operation involves creating a new node with the given value and traversing the tree to find the appropriate position. If the value is less than the current node, move to the left; if greater, move to the right. Repeat until an empty spot is found.

