Understanding the Basics

Before diving into the details of postfix to infix conversion, let’s review some fundamental concepts:

• Postfix Notation: Postfix notation, also known as Reverse Polish Notation (RPN), positions operators after their operands. For example, the expression 3 4 + represents the infix expression 3 + 4.
• Infix Notation: Infix notation is the standard arithmetic notation in which operators are placed between operands. For example, 3 + 4.

Conversion of infix to postfix in C++ using stack

Here is the key reasons of conversion of postfix to infix in C++ using stack is needed in Data Structures. Now start the traversing of postfix from left to right. At each step, perform the following actions:

Start with an empty stack.

Iterate over each character in the postfix expression from left to right.

Process each character:

• a: Operand, push onto the stack.
• b: Operand, push onto the stack.
• +: Operator, pop two operands from the stack (b and a). Construct infix expression "(a+b)" and push it onto the stack.
• c: Operand, push onto the stack.
• *: Operator, pop two operands from the stack (c and (a+b)). Construct infix expression "(c*(a+b))" and push it onto the stack.
• d: Operand, push onto the stack.
• –: Operator, pop two operands from the stack (d and (c*(a+b))). Construct infix expression "(d-(c*(a+b)))" and push it onto the stack.

After processing all characters, the top of the stack contains the final infix expression: "(d-(c*(a+b)))".

Significance of Postfix to Infix Conversion

Here are the key reasons of significance of postfix to infix Conversion in C++:

• Human Readability: Infix notation is more natural and intuitive for humans to read and understand compared to postfix notation, which is often used for machine processing.
• Expression Representation: In many scenarios, infix notation is the preferred format for representing mathematical expressions, especially in user interfaces and educational materials.
• Parsing and Evaluation: Converting postfix expressions to infix notation may be necessary for parsing algorithms and expression evaluation, especially when dealing with user input or interacting with other systems that expect infix notation.

Practical Considerations

When implementing postfix to infix conversion in real-world applications, there are several practical considerations to keep in mind:

1. Operator Precedence: Ensure that operator precedence is preserved when reconstructing the infix expression. This ensures that the resulting expression evaluates correctly.
2. Parentheses Placement: Proper placement of parentheses may be necessary to maintain the order of operations, especially when dealing with complex expressions.
3. Error Handling: Implement robust error handling to handle invalid or malformed postfix expressions gracefully. This includes detecting syntax errors and unexpected input.

Conclusion of postfix to infix C++ using stack

postfix to infix conversion is a valuable operation in various contexts within computer science and programming. By understanding the principles and techniques behind this conversion process, programmers can effectively manipulate mathematical expressions in their applications.

Source Code

Let’s break down the provided C++ code snippet that handles the postfix to infix conversion:

#include <iostream>
#include <stack>
#include <string>

using namespace std;

bool isOperator(char c) {
    return (c == '+' || c == '-' || c == '*' || c == '/');
}

string postfixToInfix(string postfix) {
    stack<string> st;

    for (int i = 0; i < postfix.length(); i++) {
        if (isOperator(postfix[i])) {
            string operand2 = st.top();
            st.pop();
            string operand1 = st.top();
            st.pop();
            string result = "(" + operand1 + postfix[i] + operand2 + ")";
            st.push(result);
        }
        else {
            string operand(1, postfix[i]);
            st.push(operand);
        }
    }

    return st.top();
}

int main() {
    string postfixExpression;
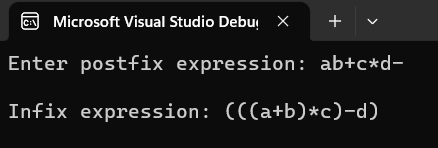
    cout << "Enter postfix expression: ";
    cin >> postfixExpression;

    string infixExpression = postfixToInfix(postfixExpression);
    cout << endl;
    cout << "Infix expression: " << infixExpression << endl;

    return 0;
}