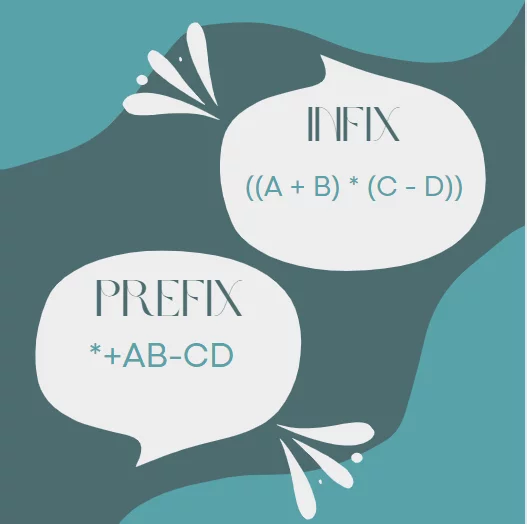
What are Infix and prefix expressions?

Prefix and infix expressions are two different ways of representing mathematical expressions.

Infix Expression: In infix notation, operators are placed between their operands. It is the standard mathematical notation that we are most familiar with. For example, the expression “3 + 4 * 5” is written in infix notation.

Prefix Expression: In prefix notation, also known as Polish notation, operators precede their operands. Each operator is placed before its operands. For example, the same expression “3 + 4 * 5” would be written as “+ 3 * 4 5” in prefix notation.

Comparison between infix and prefix

• In infix notation, operators are written between operands, making it more readable and intuitive for humans.
• In prefix notation, operators come before their operands, which can be useful for computer processing and evaluation, as it eliminates the need for parentheses to indicate the order of operations.

Conversion of prefix to infix in C++ using stack

• Step 1:Reverse the Infix Expression
  • Infix Expression: (A + B) * (C – D)
  • Reversed Infix: D – C ) * ( B + A(
• Step 2: Convert to Postfix
  • Next, we convert the reversed infix expression to postfix notation. To do this, we apply the infix to postfix conversion algorithm, but treating operators as if they were parentheses and vice versa.
    • Reversed Infix: D – C ) * ( B + A(
    • Postfix: DC-BA+*
• Step 3: Reverse the Postfix Expression
  • Now, we reverse the postfix expression to obtain the prefix expression:
    • Postfix Expression: DC-BA+* Reversed
    • Prefix: *+AB-CD
• Step 4: Final Result
  • The final result is the prefix expression:
    • Prefix Expression: *+AB-CD

Applications of infix to prefix

The applications of conversion of infix to prefix C++ using stack is given as:

1. Expression Evaluation: Prefix notation is efficient for expression evaluation, especially in applications where performance is critical.
2. Compiler Design: Converting expressions between different notations is a common task in compiler design during the parsing and optimization phases.
3. Mathematical Software: Mathematical software often deals with complex expressions, and representing them in prefix notation can simplify processing and evaluation.
4. Algorithm Design: Some algorithms, such as those used in symbolic computation, require manipulation of expressions in different notations.

Source code of infix to prefix C++ using stack

Here’s an implementation of conversion of infix to prefix in C++ using stack data structure:

#include <iostream>
#include <stack>
#include <string>
#include <algorithm>

using namespace std;

bool isOperator(char c) {
    return (c == '+' || c == '-' || c == '*' || c == '/');
}

int precedence(char op) {
    if (op == '+' || op == '-')
        return 1;
    if (op == '*' || op == '/')
        return 2;
    return 0;
}

string infixToPrefix(const string& infix) {
    stack<char> operators;
    string prefix;

    // Reverse the infix expression
    string reversedInfix = infix;
    reverse(reversedInfix.begin(), reversedInfix.end());

    for (char c : reversedInfix) {
        // If character is operand, add to the prefix string
        if (isalnum(c))
            prefix += c;
        // If character is closing parenthesis, push to the stack
        else if (c == ')')
            operators.push(c);
        // If character is opening parenthesis, pop until matching closing parenthesis
        else if (c == '(') {
            while (!operators.empty() && operators.top() != ')') {
                prefix += operators.top();
                operators.pop();
            }
            // Pop the closing parenthesis
            operators.pop();
        }
        // If character is an operator
        else if (isOperator(c)) {
            // Pop operators with higher or equal precedence and add to prefix
            while (!operators.empty() && precedence(operators.top()) >= precedence(c)) {
                prefix += operators.top();
                operators.pop();
            }
            // Push current operator to stack
            operators.push(c);
        }
    }

    // Pop remaining operators and add to prefix
    while (!operators.empty()) {
        prefix += operators.top();
        operators.pop();
    }

    // Reverse the prefix string to get the final result
    reverse(prefix.begin(), prefix.end());
    return prefix;
}

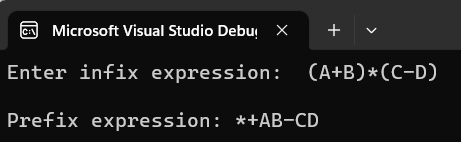
int main() {
    string infixExpression;
    cout << "Enter infix expression: ";
    cin >> infixExpression;

    string prefixExpression = infixToPrefix(infixExpression);
    cout << endl;
    cout << "Prefix expression: " << prefixExpression << endl;

    return 0;
}

Conclusion

Conversion of prefix to infix in C++ using stack is a fundamental operation in computer science with various practical applications. By understanding the conversion algorithm and implementing it in C++, you can efficiently manipulate arithmetic expressions in different notations. I hope this blog post has provided you with insights into infix to prefix expression conversion and its significance in programming and computational tasks. Feel free to experiment with the provided code and explore further applications of expression manipulation!