8 Puzzle Solver Project Using A* Search in C++(2025)

Explore the 8 Puzzle Solver Project Using A* Search in C++ to solve the classic 8-puzzle problem. Learn how the A* search algorithm and Manhattan Distance heuristic work, with step-by-step explanations and insights into why this approach is effective.

Table of Contents

Key Concepts

**1. A* Search Algorithm**

A* is a pathfinding algorithm that combines the strengths of uniform-cost search and greedy best-first search. It uses a heuristic function to estimate the cost to reach the goal from a given state and prioritizes states with the lowest total cost:

Total Cost = Heuristic Cost + Path Cost
Heuristic Cost: An estimate of the cost to reach the goal from the current state.
Path Cost: The cost to reach the current state from the initial state (depth in the search tree).

A* is guaranteed to find the shortest path to the goal if the heuristic is admissible (never overestimates the true cost).

NOTE

You can get its code from my GitHub repository

GitHub repository

2. Manhattan Distance Heuristic

The Manhattan Distance is a common heuristic for the 8-puzzle problem. It calculates the sum of the horizontal and vertical distances of each tile from its position in the goal state. For example:

If a tile is at position (1, 2) in the current state and its goal position is (2, 1), its Manhattan Distance is |1-2| + |2-1| = 2.

This heuristic is admissible because it never overestimates the number of moves required to solve the puzzle.

How the Algorithm Works

1. State Representation

Each state of the puzzle is represented by:

A 3×3 grid (the current arrangement of tiles).
The position of the empty tile (denoted by 0).
The heuristic cost (Manhattan Distance).
The depth in the search tree (number of moves from the initial state).
A pointer to the parent state (used to reconstruct the solution path).

The states are compared based on their total cost (heuristic cost + depth), ensuring that the algorithm prioritizes the most promising paths.

8 Puzzle Solver Project Using A* Search in C++

What is Manhattan Distance?

The Manhattan Distance is the sum of the horizontal and vertical distances between the current position of each tile and its goal position. It is called “Manhattan” because it resembles the distance you would walk in a grid-like city (like Manhattan, New York), where you can only move horizontally or vertically, not diagonally.

For example:

If a tile is at position (1, 1) in the current state and its goal position is (2, 2), the Manhattan Distance is:

|1 – 2| + |1 – 2| = 1 + 1 = 2

Why Use Manhattan Distance as a Heuristic?

Admissibility:
- The Manhattan Distance is admissible, meaning it never overestimates the actual cost to reach the goal. This guarantees that the A* algorithm will find the optimal solution.
Efficiency:
- By prioritizing states with lower heuristic costs, the algorithm avoids exploring unnecessary paths, making it faster than brute-force methods like BFS or DFS.

2. What is a Heuristic?

The heuristic approach in this code is based on the Manhattan Distance, which is a common heuristic used in puzzle-solving algorithms like the A* algorithm.

A heuristic is an estimate of how close a given state is to the goal state. It helps the algorithm prioritize which states to explore next, making the search process more efficient.

For example:

If the current state is:

  1 2 3
  8 0 6
  4 7 5

And the goal state is:

  1 2 3
  4 5 6
  7 8 0

Heuristic Calculation:

Tile 1 is already in the correct position: cost = 0.
Tile 2 is already in the correct position: cost = 0.
Tile 3 is already in the correct position: cost = 0.
Tile 8 is at (1, 0) but should be at (2, 1): cost = |1-2| + |0-1| = 1 + 1 = 2.
Tile 5 is already in the correct position: cost = 0.
Tile 6 is already in the correct position: cost = 0.
Tile 4 is at (2, 0) but should be at (1, 0): cost = |2-1| + |0-0| = 1 + 0 = 1.
Tile 7 is at (2, 1) but should be at (2, 0): cost = |2-2| + |1-0| = 0 + 1 = 1.

Total Heuristic Cost = 0 + 0 + 0 + 2 + 0 + 0 + 1 + 1 = 4.

Why is the Heuristic Important?

Without the heuristic, the algorithm would explore all possible states blindly, which is inefficient.
The heuristic guides the algorithm toward the goal, reducing the number of states it needs to explore.

How is the Heuristic Used in the Code?

Heuristic Calculation:

The calculateCost function computes the Manhattan Distance for all tiles (except the empty tile 0) in the current state compared to their positions in the goal state.
It sums up the distances for all tiles to get the total heuristic cost.

Priority Queue:

The algorithm uses a priority queue to explore states with the lowest total cost first.
The total cost is the sum of:
- Heuristic Cost (cost): Estimated distance to the goal.
- Level (level): Number of moves taken to reach the current state (depth in the search tree).

This ensures that the algorithm prioritizes states that are closer to the goal (low heuristic cost) and have taken fewer moves (low level).

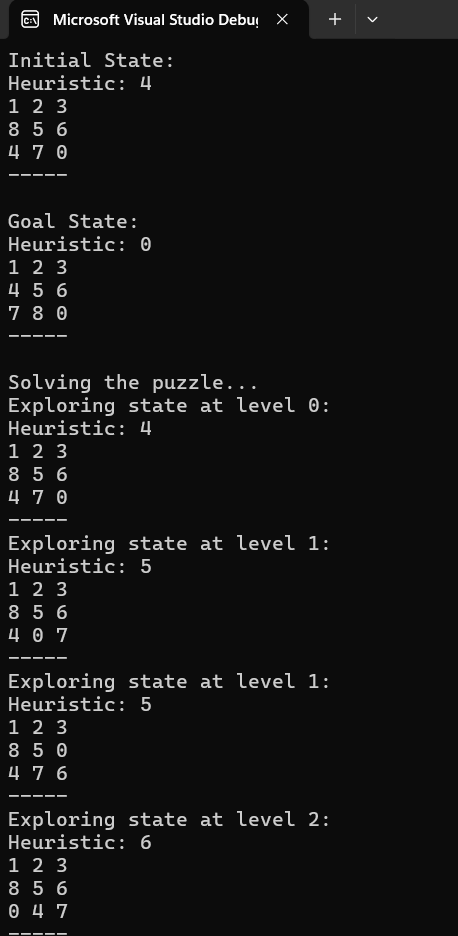
3. Exploring States

The algorithm uses a priority queue to explore states in order of their total cost. At each step:

Initial State:
- The algorithm starts with the initial state of the puzzle.
Explore States:
- It generates all possible next states by moving the empty tile (0) in all valid directions (up, down, left, right).
- For each new state, it calculates the heuristic cost (Manhattan Distance) and adds it to the priority queue.
Goal Check:
- If a state’s heuristic cost is 0, it means all tiles are in their goal positions, and the puzzle is solved.
Backtracking:
- Once the goal is reached, the algorithm backtracks using the parent pointer to reconstruct the solution path.

This process continues until the goal state is reached or all possibilities are exhausted.

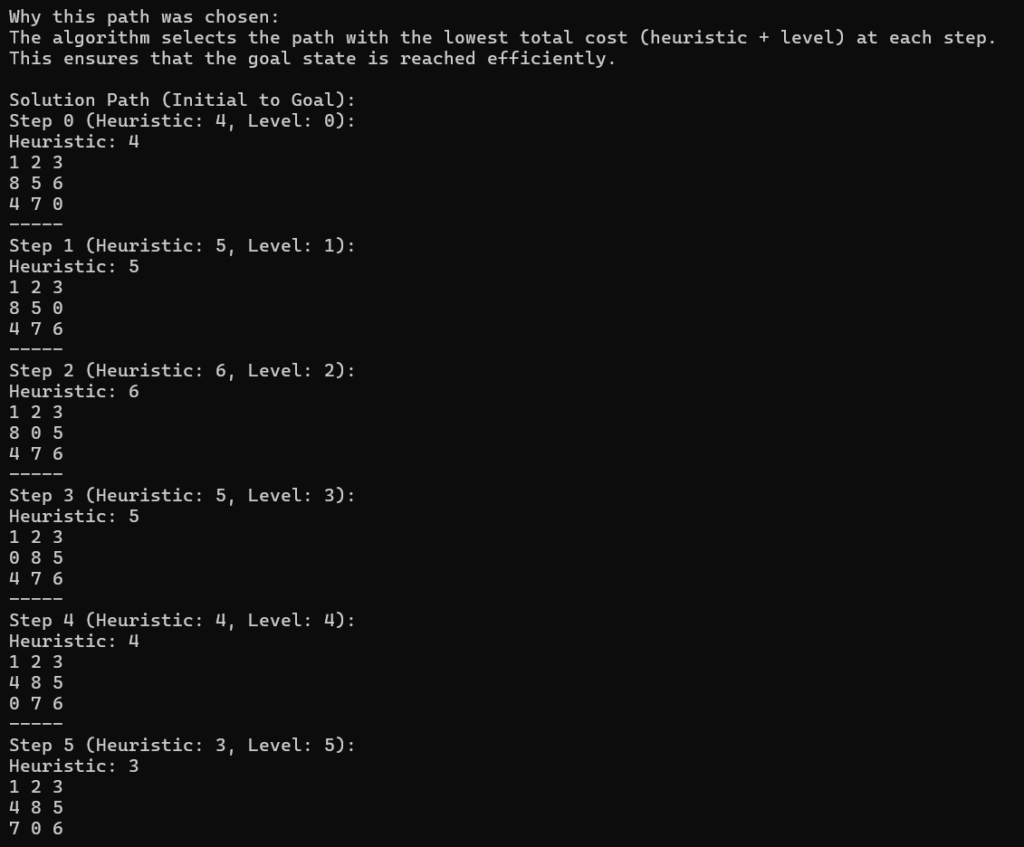
4. Solution Path

Once the goal state is reached, the algorithm backtracks using the parent pointers to reconstruct the solution path. This path shows the sequence of moves required to solve the puzzle.

Why This Approach Works

The A* search algorithm is efficient because it balances exploration and exploitation:

It explores states that are closer to the goal (guided by the heuristic).
It avoids exploring unpromising paths (thanks to the priority queue).

The Manhattan Distance heuristic is particularly effective because it provides a good estimate of the remaining cost without overestimating it.

Conclusion

The A* search algorithm, combined with the Manhattan Distance heuristic, provides an efficient and effective way to solve the 8-puzzle problem. By prioritizing states that are closer to the goal and avoiding unnecessary exploration, the algorithm quickly finds the shortest solution path.

Source code of 8 Puzzle Solver Project Using A* Search in C++

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <set>

using namespace std;

const int N = 3;

struct State {
    vector<vector<int>> board;
    int x, y; // Position of the empty tile (0)
    int cost; // Heuristic cost (Manhattan Distance)
    int level; // Depth in the search tree
    State* parent; // Pointer to parent state for backtracking

    bool operator<(const State& other) const {
        return (cost + level) > (other.cost + other.level); // Lower cost + level has higher priority
    }
};

// Calculate Manhattan Distance heuristic
int calculateCost(const vector<vector<int>>& board, const vector<vector<int>>& goal) {
    int cost = 0;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            if (board[i][j] != 0) { // Ignore the empty tile
                // Find the position of the tile in the goal state
                for (int k = 0; k < N; k++) {
                    for (int l = 0; l < N; l++) {
                        if (board[i][j] == goal[k][l]) {
                            cost += abs(i - k) + abs(j - l); // Manhattan Distance
                            break;
                        }
                    }
                }
            }
        }
    }
    return cost;
}

bool isSafe(int x, int y) {
    return (x >= 0 && x < N && y >= 0 && y < N);
}

void printBoard(const vector<vector<int>>& board, int heuristic) {
    cout << "Heuristic: " << heuristic << "\n";
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            cout << board[i][j] << " ";
        }
        cout << endl;
    }
    cout << "-----\n";
}

void printSolutionPath(State* goalState) {
    vector<State*> path;
    State* current = goalState;

    // Backtrack from goal to initial state
    while (current) {
        path.push_back(current);
        current = current->parent;
    }

    // Print the solution path in reverse order
    reverse(path.begin(), path.end());

    // Explanation message
    cout << "\nWhy this path was chosen:\n";
    cout << "The algorithm selects the path with the lowest total cost (heuristic + level) at each step.\n";
    cout << "This ensures that the goal state is reached efficiently.\n\n";

    cout << "Solution Path (Initial to Goal):\n";
    int step = 0;
    for (State* state : path) {
        cout << "Step " << step++ << " (Heuristic: " << state->cost << ", Level: " << state->level << "):\n";
        printBoard(state->board, state->cost);
    }
    cout << "Solution completed in " << path.size() - 1 << " steps.\n";
}

bool solvePuzzle(const vector<vector<int>>& initial, const vector<vector<int>>& goal, int x, int y) {
    priority_queue<State> pq;
    set<vector<vector<int>>> visited;

    // Root node (initial state)
    State* root = new State{ initial, x, y, calculateCost(initial, goal), 0, nullptr };
    pq.push(*root);
    visited.insert(initial);

    int row[] = { 1, 0, -1, 0 }; // Directions: Down, Left, Up, Right
    int col[] = { 0, -1, 0, 1 };

    while (!pq.empty()) {
        State current = pq.top();
        pq.pop();

        // Print the current state and its heuristic value
        cout << "Exploring state at level " << current.level << ":\n";
        printBoard(current.board, current.cost);

        // Check if the current state is the goal state
        if (current.cost == 0) {
            cout << "\nGoal State Reached at Level " << current.level << ":\n";
            printBoard(current.board, current.cost);
            printSolutionPath(&current);
            return true;
        }

        // Generate child states
        for (int i = 0; i < 4; i++) {
            int newX = current.x + row[i];
            int newY = current.y + col[i];

            if (isSafe(newX, newY)) {
                vector<vector<int>> newBoard = current.board;
                swap(newBoard[current.x][current.y], newBoard[newX][newY]);

                // Check if the new state has already been visited
                if (visited.find(newBoard) == visited.end()) {
                    int newCost = calculateCost(newBoard, goal);
                    State* child = new State{ newBoard, newX, newY, newCost, current.level + 1, new State(current) };
                    pq.push(*child);
                    visited.insert(newBoard);
                }
            }
        }
    }

    cout << "No solution exists." << endl;
    return false;
}

int main() {
    // Initial state
    vector<vector<int>> initial = { {1, 2, 3}, {8, 5, 6}, {4, 7, 0} };

    // Goal state
    vector<vector<int>> goal = { {1, 2, 3}, {4, 5, 6}, {7, 8, 0} };

    // Initial position of the empty tile (0)
    int x = 2, y = 2;

    cout << "Initial State:\n";
    printBoard(initial, calculateCost(initial, goal));
    cout << "\nGoal State:\n";
    printBoard(goal, 0);
    cout << "\nSolving the puzzle...\n";

    solvePuzzle(initial, goal, x, y);

    return 0;
}

8 Puzzle Solver Project Using A* Search in C++